桶排序

桶排序（bucket sort）是分治策略的一个典型应用。它通过设置一些具有大小顺序的桶，每个桶对应一个数据范围，将数据平均分配到各个桶中；然后，在每个桶内部分别执行排序；最终按照桶的顺序将所有数据合并。

本质是先划分好区间，然后在区间中进行排序。

算法流程

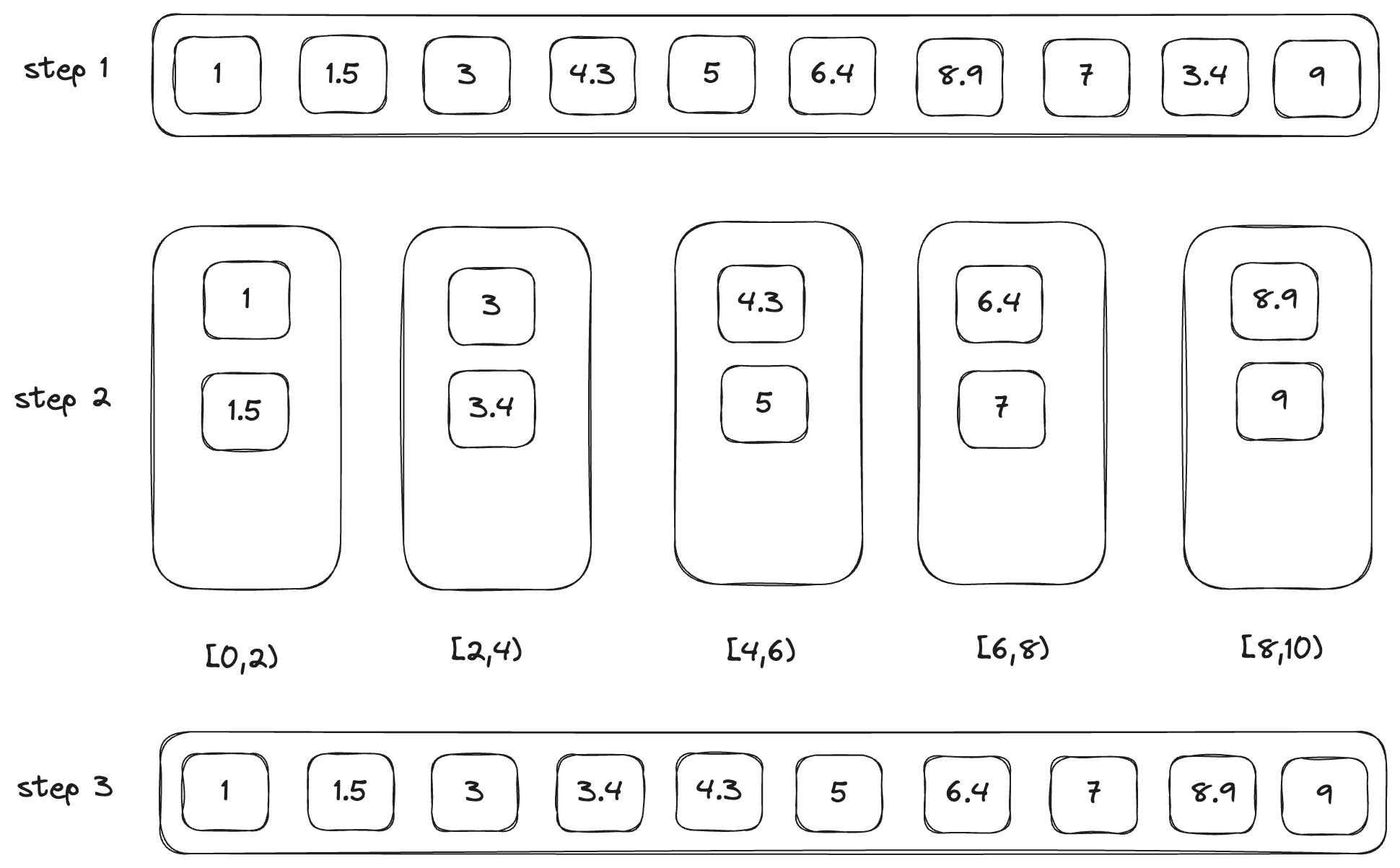
有一个数组，范围在 [1, 10] 中，整体流程如下。

1. 初始化 K 个桶，将 数组元素分配到对应的桶中。
2. 对每个桶中的元素分别进行排序。
3. 按照桶从小到大顺序进行合并。

代码

function bucketSort(nums: number[]): void {
  const k = nums.length / 2;
  const buckets: number[][] = [];
  for (let i = 0; i < k; i++) {
    buckets.push([]);
  }

  for (const num of nums) {
    // 输入数据范围为 [0, 1)，使用 num * k 映射到索引范围 [0, k-1]
    const i = Math.floor(num * k);
    // 将 num 添加进桶 i
    buckets[i].push(num);
  }

  for (const bucket of buckets) {
    // 使用内置排序函数，也可以替换成其他排序算法
    bucket.sort((a, b) => a - b);
  }

  let i = 0;

  for (const bucket of buckets) {
    for (const num of bucket) {
      nums[i++] = num;
    }
  }
}

算法特性

桶排序适用于处理体量很大的数据。例如，输入数据包含 100 万个元素，由于空间限制，系统内存无法一次性加载所有数据。此时，可以将数据分成 1000 个桶，然后分别对每个桶进行排序，最后将结果合并。

• 时间复杂度为  𝑂(𝑛+𝑘) ：假设元素在各个桶内平均分布，那么每个桶内的元素数量为  𝑛𝑘 。假设排序单个桶使用  𝑂(𝑛𝑘log⁡𝑛𝑘)  时间，则排序所有桶使用  𝑂(𝑛log⁡𝑛𝑘)  时间。当桶数量  𝑘  比较大时，时间复杂度则趋向于  𝑂(𝑛) 。合并结果时需要遍历所有桶和元素，花费  𝑂(𝑛+𝑘)  时间。
• 自适应排序：在最差情况下，所有数据被分配到一个桶中，且排序该桶使用  𝑂(𝑛2)  时间。
• 空间复杂度为  𝑂(𝑛+𝑘)、非原地排序：需要借助  𝑘  个桶和总共  𝑛  个元素的额外空间。
• 桶排序是否稳定取决于排序桶内元素的算法是否稳定。

参考

• Hello算法-桶排序