回溯算法
回溯算法是一种用于寻找所有(或部分)解的一种算法。它通过逐步构建解决方案,并在发现部分解决方案不能通向最终解时回退(即“回溯”),尝试其他可能的路径。
以下是回溯算法的基本思想和步骤:
基本思想
回溯算法通常采用深度优先搜索来遍历解决问题。在每一步选择中,尝试每一种可能的选择,当发现某个选择不能得到有效解时,回退到上一步,尝试其他选择。
算法步骤
- 选择路径:在当前步骤选择一个可能的选择。
- 剪枝判断:检查当前选择是否满足问题的约束条件。如果不满足,则放弃当前选择(即剪枝)。
- 递归处理:若当前选择满足条件,则继续递归处理下一个步骤。
- 回溯:若通过当前选择不能得到解,撤销选择并返回上一步,尝试其他选择。
常用术语
| 名词 | 定义 |
|---|---|
| 解(solution) | 解是满足问题特定条件的答案,可能有一个或多个 |
| 约束条件(constraint) | 约束条件是问题中限制解的可行性的条件,通常用于剪枝 |
| 状态(state) | 状态表示问题在某一时刻的情况,包括已经做出的选择 |
| 尝试(attempt) | 尝试是根据可用选择来探索解空间的过程,包括做出选择,更新状态,检查是否为解 |
| 回退(backtracking) | 回退指遇到不满足约束条件的状态时,撤销前面做出的选择,回到上一个状态 |
| 剪枝(pruning) | 剪枝是根据问题特性和约束条件避免无意义的搜索路径的方法,可提高搜索效率 |
举个例子 🌰
下面用二叉搜索树来举个例子
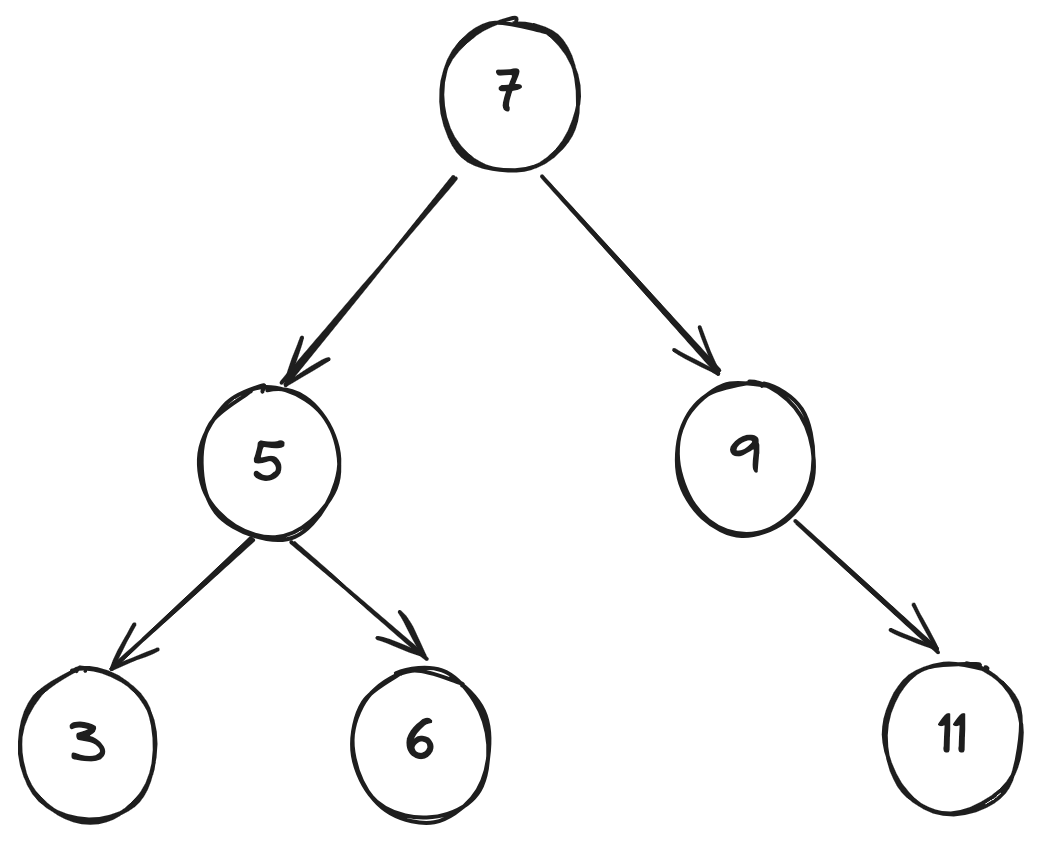
回退
场景:需要记录树节点值为奇数的节点。
在这个过程中,很明显是需要对整个树遍历的,在这个过程中,就会涉及到回退。
比如,我们通过中序遍历已经遍历到 3 节点了
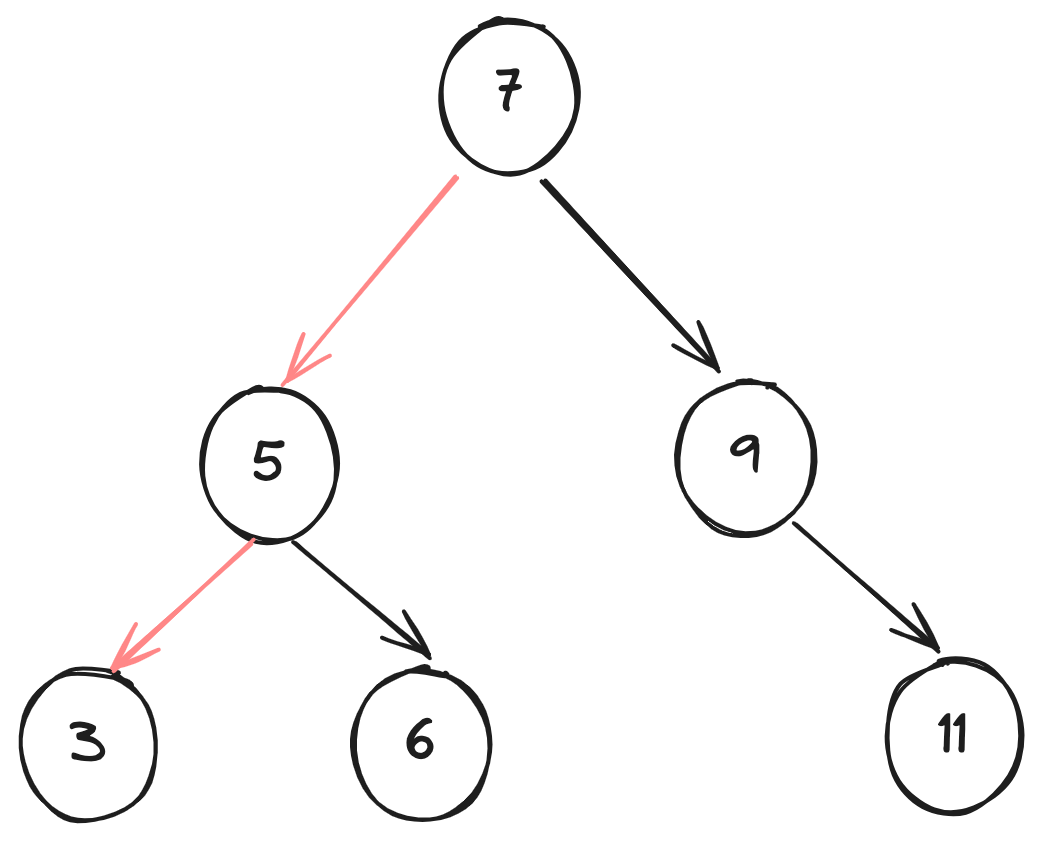
这个时候,我们进行会退到 5 节点, 其实这里也算回溯。
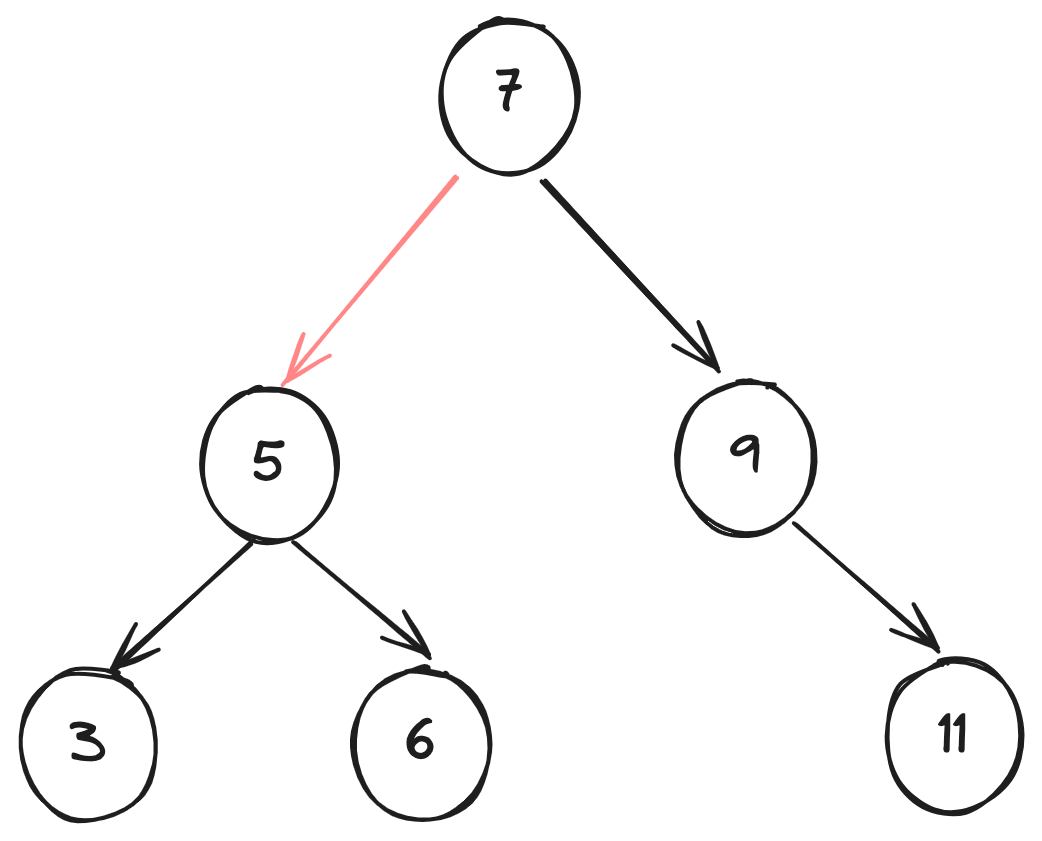
剪枝
场景:需要记录树节点值为大于 5 的节点。
在这个过程中,我们使用前序遍历,同时,我们这里是一个二叉搜索树。 这里,遍历到 5 了之后,我们可以把 5 进行剪枝操作。
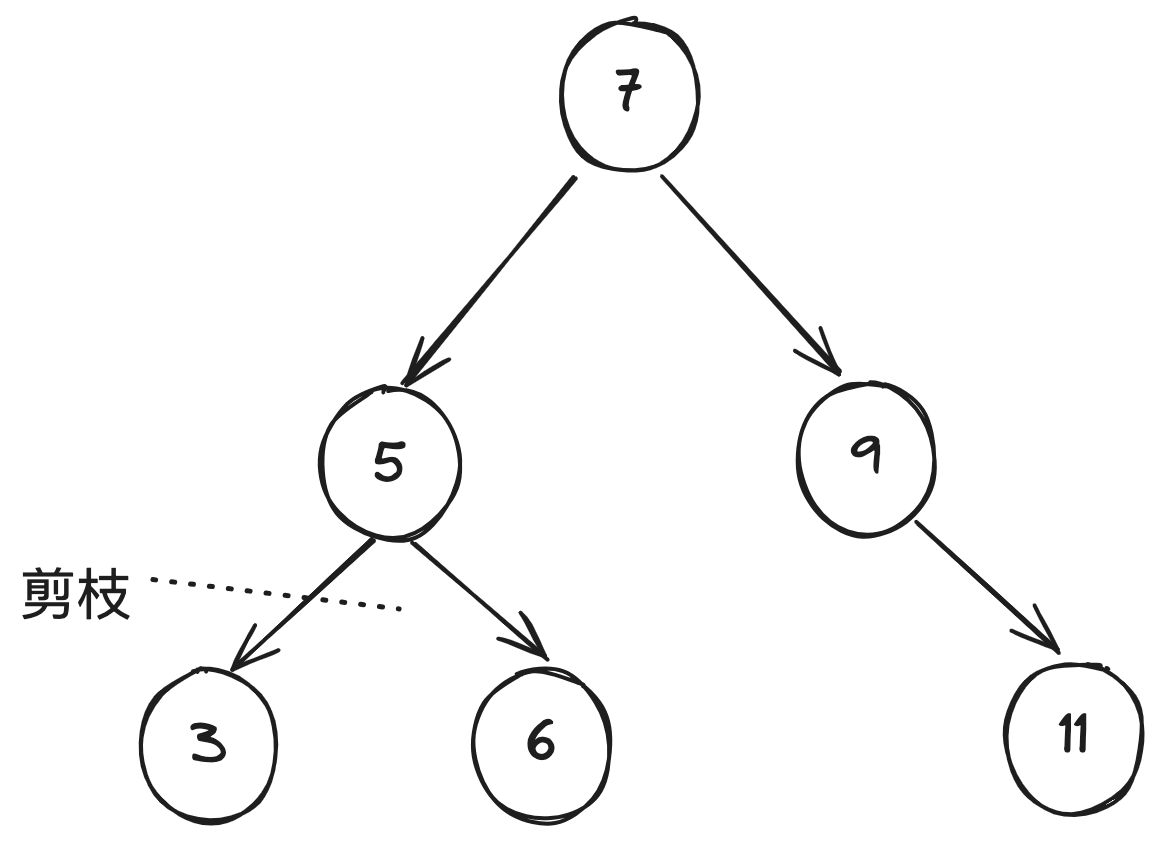
优点与局限性
回溯算法本质上是一种深度优先搜索算法,它尝试所有可能的解决方案直到找到满足条件的解。这种方法的优点在于能够找到所有可能的解决方案,而且在合理的剪枝操作下,具有很高的效率。
然而,在处理大规模或者复杂问题时,回溯算法的运行效率可能难以接受。
- 时间:回溯算法通常需要遍历状态空间的所有可能,时间复杂度可以达到指数阶或阶乘阶。
- 空间:在递归调用中需要保存当前的状态(例如路径、用于剪枝的辅助变量等),当深度很大时,空间需求可能会变得很大。
即便如此,回溯算法仍然是某些搜索问题和约束满足问题的最佳解决方案。对于这些问题,由于无法预测哪些选择可生成有效的解,因此我们必须对所有可能的选择进行遍历。在这种情况下,关键是如何优化效率,常见的效率优化方法有两种。
- 剪枝:避免搜索那些肯定不会产生解的路径,从而节省时间和空间。
- 启发式搜索:在搜索过程中引入一些策略或者估计值,从而优先搜索最有可能产生有效解的路径。
回溯算法应用
回溯算法可用于解决许多搜索问题、约束满足问题和组合优化问题。如搜索问题、约束满足问题、组合优化问题。
回溯在大多情况下是基于 DFS(深度优先搜索)去做的。