贪心算法

贪心算法（greedy algorithm）是一种常见的解决优化问题的算法，其基本思想是在问题的每个决策阶段，都选择当前看起来最优的选择，即贪心地做出局部最优的决策，以期获得全局最优解。贪心算法简洁且高效，在许多实际问题中有着广泛的应用。

贪心算法和动态规划都常用于解决优化问题。它们之间存在一些相似之处，比如都依赖最优子结构性质，但工作原理不同。

动态规划会根据之前阶段的所有决策来考虑当前决策，并使用过去子问题的解来构建当前子问题的解。
贪心算法不会考虑过去的决策，而是一路向前地进行贪心选择，不断缩小问题范围，直至问题被解决。

给定 𝑛 种硬币，第 𝑖 种硬币的面值为 𝑐𝑜𝑖𝑛𝑠[𝑖−1] ，目标金额为 𝑎𝑚𝑡 ，每种硬币可以重复选取，问能够凑出目标金额的最少硬币数量。如果无法凑出目标金额，则返回 −1 。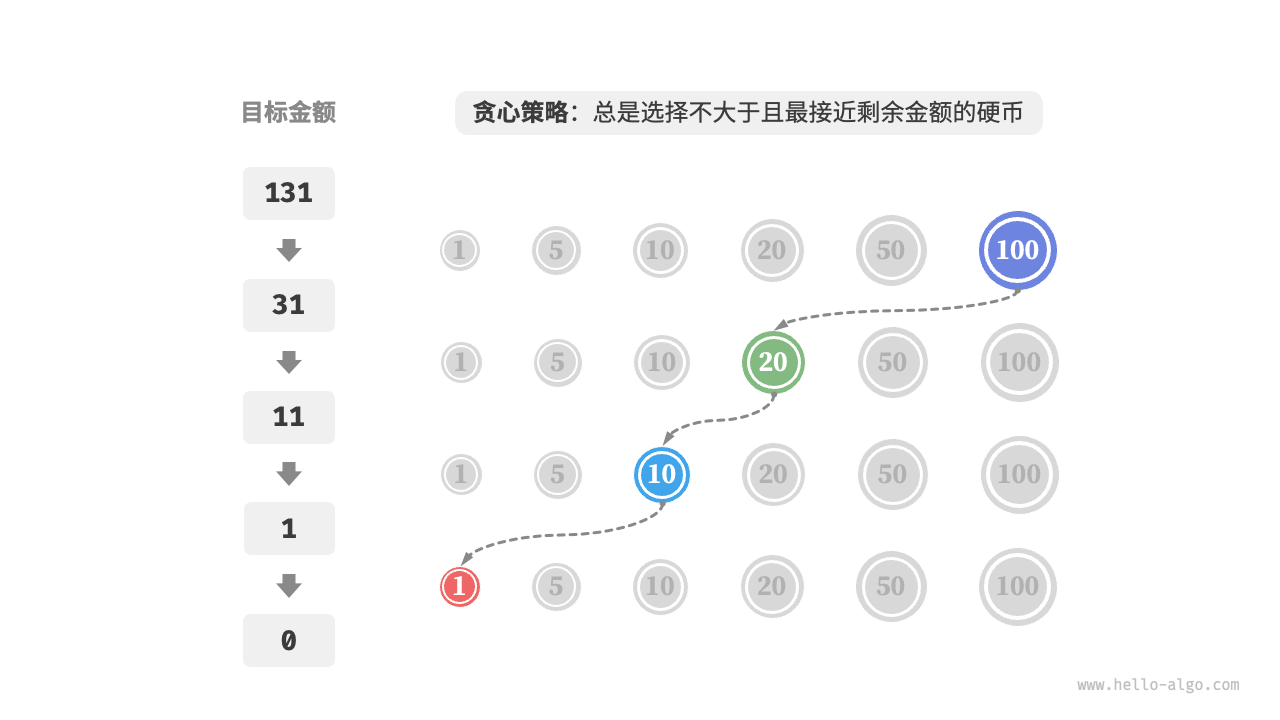

const coinChangeGreedy = (coins: number[], amt: number): number => {
  let i  = coins.length - 1;
  let count = 0;
  while(amt > 0) {
    while(i > 0 && coins[i] > amt) {
      i--;
    }
    amt -= coins[i];
    count++;
  }
  return amt === 0 ? count : -1;
}

贪心算法作为一种常用的算法设计策略，既有其显著的优点，也存在一些局限性。以下是对贪心算法优缺点的详细分析：

优缺点

优点

简单易懂：贪心算法的思想和实现通常比较简单。由于它在每一步只做出一个选择，因此算法流程易于理解和编写。
高效性：贪心算法通常具有较低的时间复杂度。例如，解决活动选择问题的贪心算法在O(n log n)时间内完成（假设活动已经排序）。在一些问题中，贪心算法比其他复杂算法更高效。
局部最优性：在某些特定类型的问题中，贪心算法可以直接得出全局最优解。例如，最小生成树问题中的Kruskal和Prim算法，以及Dijkstra算法解决单源最短路径问题。
空间复杂度低：贪心算法通常不需要大量的辅助空间，只需要存储当前的选择结果和一些临时变量。

缺点

全局最优性不能保证：贪心算法只关注每一步的局部最优选择，有些问题可能通过这种方式无法得到全局最优解。背包问题和图的着色问题就是典型的例子。
需要问题特性支持：贪心算法适用于具有贪心选择性质和最优子结构性质的问题。对于不具备这些性质的问题，贪心算法可能无法应用或只能得到次优解。
不适用于所有问题：许多复杂的优化问题，例如一般的旅行商问题（TSP），贪心算法无法提供有效的解决方案，往往需要其他算法（如动态规划、回溯算法）来求解。
可能需要预处理：在某些情况下，贪心算法需要对输入数据进行预处理，如排序。这些操作会增加额外的时间复杂度。

贪心算法特性

贪心选择性质（Greedy Choice Property）：贪心算法在每一步选择中都采取当前最优的选项。即每一步都做出局部最优选择，以期最终能得到全局最优解。贪心选择性质是贪心算法的核心思想之一，它假设每一步的局部最优选择会导致全局最优解。
最优子结构性质（Optimal Substructure Property）：问题的最优解可以通过其子问题的最优解递归地构建出来。也就是说，一个问题的最优解包含了其子问题的最优解。具有最优子结构性质的问题通常可以通过贪心算法或动态规划来解决。
选择的不可撤销性（Irrevocability）：一旦在某一步做出选择，就不会再更改。贪心算法的每一步选择都是最终的，不会进行回溯。这意味着每一步选择都是独立的，且对后续步骤有直接影响。
局部最优性（Local Optimality）：贪心算法在每一步选择中都尝试找到当前最优解，并基于这个局部最优解继续求解问题。它不考虑整体问题的全局情况，而是逐步构建解决方案。

步骤

贪心问题的解决流程大体可分为以下三步。

问题分析：梳理与理解问题特性，包括状态定义、优化目标和约束条件等。这一步在回溯和动态规划中都有涉及。
确定贪心策略：确定如何在每一步中做出贪心选择。这个策略能够在每一步减小问题的规模，并最终解决整个问题。
正确性证明：通常需要证明问题具有贪心选择性质和最优子结构。这个步骤可能需要用到数学证明，例如归纳法或反证法等。

贪心算法 ​

优缺点 ​

优点 ​

缺点 ​

贪心算法特性 ​

步骤 ​

贪心算法

优缺点

优点

缺点

贪心算法特性

步骤