0-1 背包问题

背包问题是一个非常好的动态规划入门题目，是动态规划中最常见的问题形式。其具有很多变种，例如 0-1 背包问题、完全背包问题、多重背包问题等。

在本节中，我们先来求解最常见的 0-1 背包问题。

观察图 14-17 ，由于物品编号𝑖从1开始计数，数组索引从0开始计数，因此物品𝑖对应重量 𝑤𝑔𝑡[𝑖−1] 和价值 𝑣𝑎𝑙[𝑖−1] 。

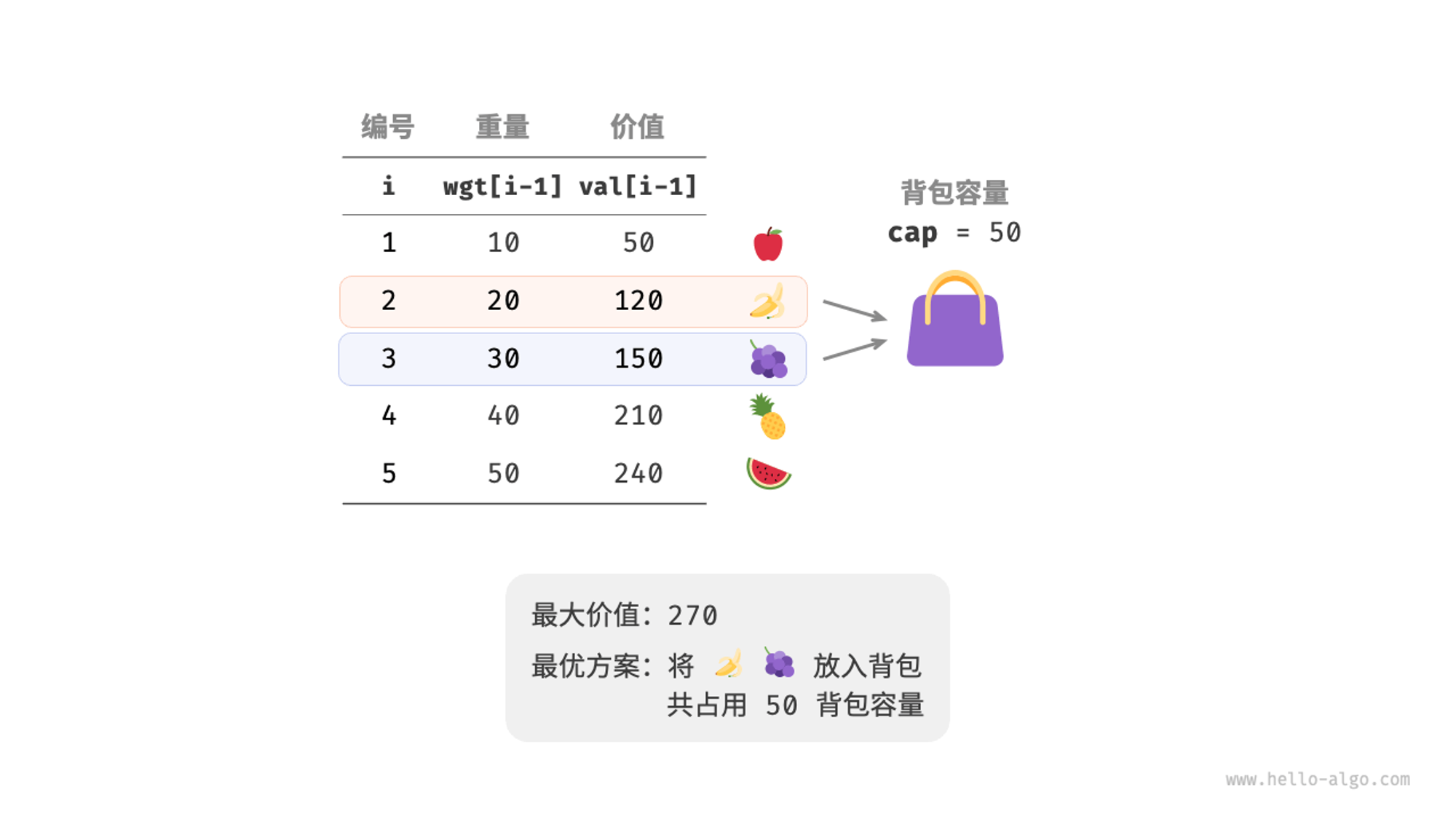
我们可以将 0-1 背包问题看作一个由 𝑛 轮决策组成的过程，对于每个物体都有不放入和放入两种决策，因此该问题满足决策树模型。

该问题的目标是求解“在限定背包容量下能放入物品的最大价值”，因此较大概率是一个动态规划问题。

第一步：思考每轮的决策，定义状态，从而得到 𝑑𝑝 表

对于每个物品来说，不放入背包，背包容量不变；放入背包，背包容量减小。由此可得状态定义：当前物品编号 𝑖 和背包容量 𝑐 ，记为 [𝑖,𝑐] 。

状态 [𝑖,𝑐] 对应的子问题为：前 𝑖 个物品在容量为 𝑐 的背包中的最大价值，记为 𝑑𝑝[𝑖,𝑐] 。

待求解的是 𝑑𝑝[𝑛,𝑐𝑎𝑝] ，因此需要一个尺寸为 (𝑛+1)×(𝑐𝑎𝑝+1) 的二维 𝑑𝑝 表。

第二步：找出最优子结构，进而推导出状态转移方程

当我们做出物品 i 的决策后，剩余的是前 i-1 物品决策的子问题，再分以下两种情况。

不放入物品 i: 背包容量不变，状态变化为 [i-1, c]
放入物品 i：背包容器减少𝑤𝑔𝑡[𝑖−1]，价值增加𝑣𝑎𝑙[𝑖−1]，状态变化为[𝑖−1,𝑐−𝑤𝑔𝑡[𝑖−1]]。

上述分析向我们揭示了本题的最优子结构：最大价值 𝑑𝑝[𝑖,𝑐] 等于不放入物品 𝑖 和放入物品 𝑖 两种方案中价值更大的那一个。由此可推导出状态转移方程：

tsx

dp[i,c] = max(dp[i-1, c], dp[i-1, c-wgt[i-1]] + val[i-1])

需要注意的是，若当前物品重量𝑤𝑔𝑡[𝑖−1]超出剩余背包容量𝑐，则只能选择不放入背包。

第三步：确定边界条件和状态转移顺序

当无物品或背包容量为 0 时最大价值为 0 ，即首列 𝑑𝑝[𝑖,0] 和首行 𝑑𝑝[0,𝑐] 都等于 0 。

当前状态 [𝑖,𝑐] 从上方的状态 [𝑖−1,𝑐] 和左上方的状态 [𝑖−1,𝑐−𝑤𝑔𝑡[𝑖−1]] 转移而来，因此通过两层循环正序遍历整个 𝑑𝑝 表即可。

根据以上分析，我们接下来按顺序实现暴力搜索、记忆化搜索、动态规划解法。

暴力搜索

搜索代码包含以下要素。

递归参数：状态 [𝑖,𝑐]。
返回值：子问题的解 𝑑𝑝[𝑖,𝑐] 。
终止条件：当物品编号越界 𝑖=0 或背包剩余容量为0 时，终止递归并返回价值 0。
剪枝：若当前物品重量超出背包剩余容量，则只能选择不放入背包。

tsx

function knapsackDFS(
    wgt: Array<number>,
    val: Array<number>,
    i: number,
    c: number
): number {
  if(i === 0 || c === 0) {
    return 0;
  }
  
  if(wgt[i - 1] > c) {
    return knapsackDFS(wgt, val, i - 1, c);
  }
  
  const no = knapsackDFS(wgt, val, i - 1, c);
  const yes = knapsackDFS(wgt, val, i - 1, c - wgt[i - 1]) + val[i - 1];
  return Math.max(no, yes);
}

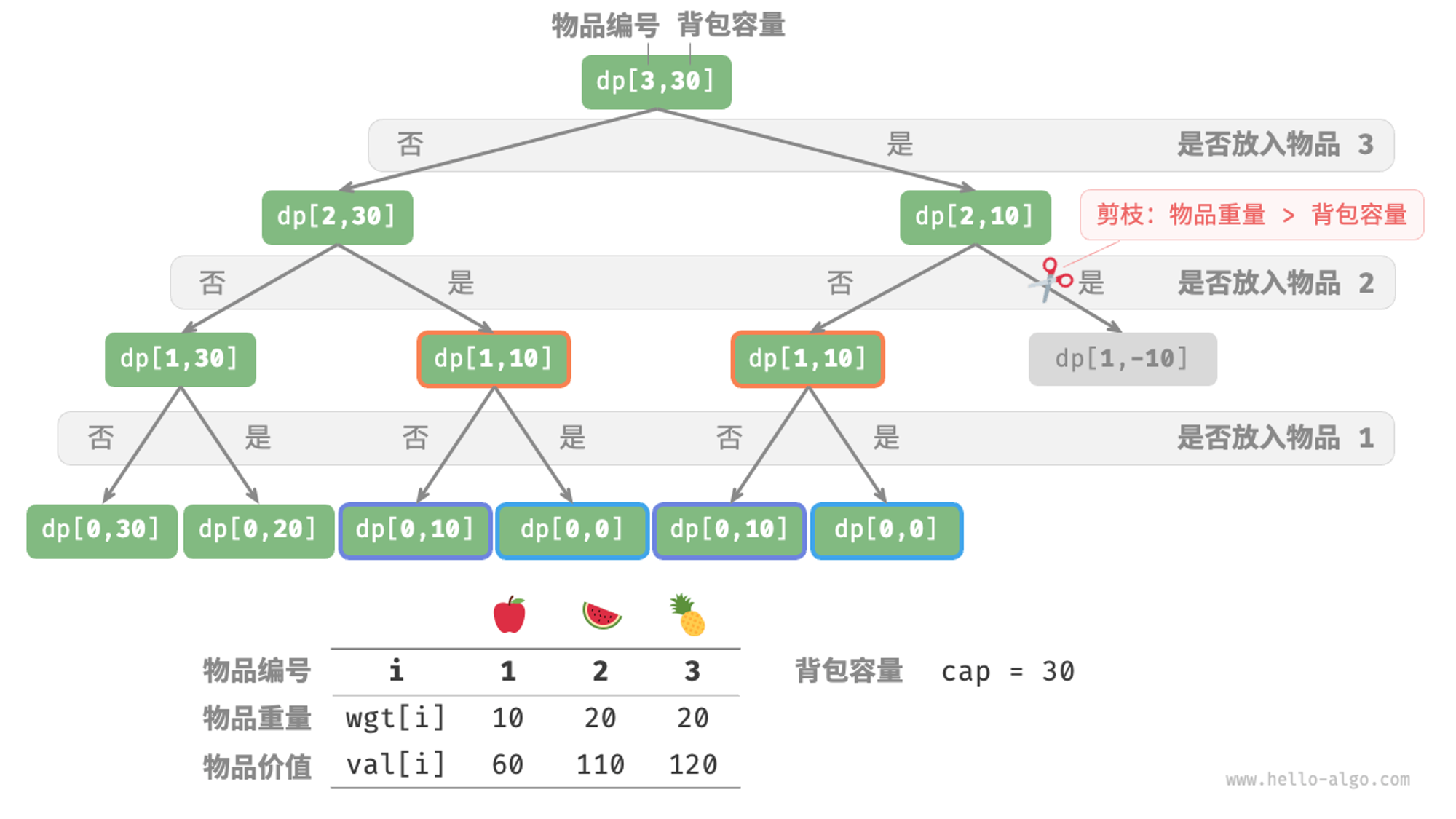
如图 14-18 所示，由于每个物品都会产生不选和选两条搜索分支，因此时间复杂度为 𝑂(2𝑛) 。

观察递归树，容易发现其中存在重叠子问题，例如 𝑑𝑝[1,10] 等。而当物品较多、背包容量较大，尤其是相同重量的物品较多时，重叠子问题的数量将会大幅增多。

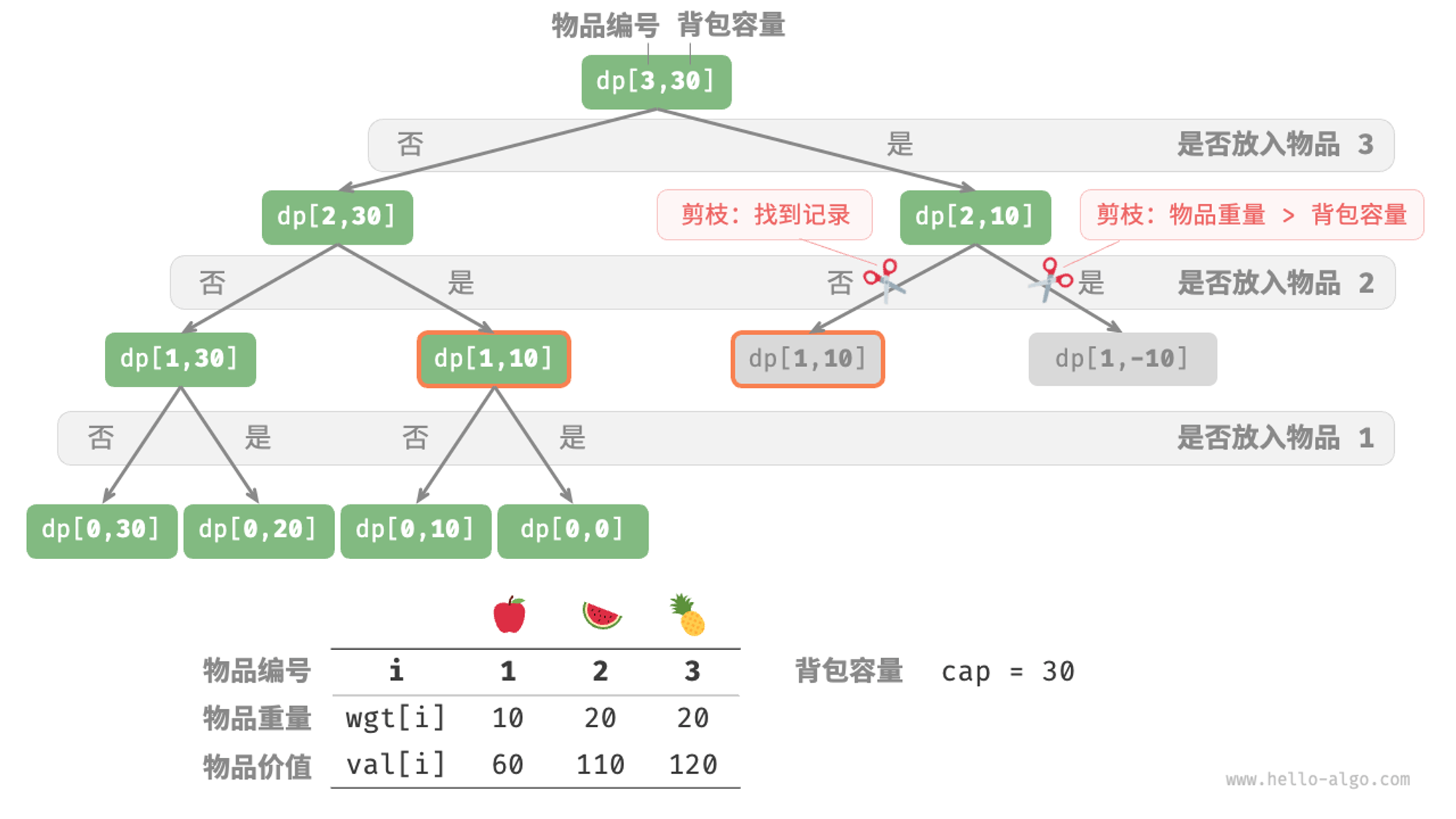
记忆化搜索

tsx

function knapsackDFSMem(
    wgt: Array<number>,
    val: Array<number>,
    mem: Array<Array<number>>,
    i: number,
    c: number
): number {
  if(i === 0 || c === 0) {
	  return 0;
	}
	
	if (mem[i][c]) {
	  return mem[i][c];
	}
	
	if(wgt[i - 1] > c) {
	  return knapsackDFSMem(wgt, val, mem, i - 1, c);
	}
	
	// 计算不放入和放入物品 i 的最大价值
  const no = knapsackDFSMem(wgt, val, mem, i - 1, c);
  const yes = knapsackDFSMem(wgt, val, mem, i - 1, c - wgt[i - 1]) + val[i - 1];
        
  return Math.max(no, yes);
}

动态规划

接着我们采用动态规划。

tsx

function knapsackDP(
    wgt: Array<number>,
    val: Array<number>,
    cap: number
): number {
  const n = wgt.length;
  // 初始化 dp 表
  const dp = Array.from({ length: n + 1 }, () =>
    Array.from({ length: cap + 1 }, () => 0)
  );
  
  // 初始化 dp 表，dp[i][j] 表示前 i 个物品在容量为 j 时的最大价值
  for(let i = 1; i <= n; i++) {
    for(let c = 1; c <= cap; c++) {
      // 当前物品重量大于当前容量，不选这个物品
      if (wgt[i - 1] > c) {
        dp[i][c] = dp[i - 1][c];
      } else {
        dp[i][c] = Math.max(
          dp[i - 1][c],  // 不选当前物品
          dp[i - 1][c - wgt[i - 1]] + val[i - 1]  // 选当前物品
        );
      }
    }
  }
  
  
  return dp[n][cap]
}

参考

https://www.hello-algo.com/chapter_dynamic_programming/knapsack_problem/#2

0-1 背包问题 ​

暴力搜索 ​

记忆化搜索 ​

动态规划 ​

参考 ​

0-1 背包问题

暴力搜索

记忆化搜索

动态规划

参考