最大容量问题

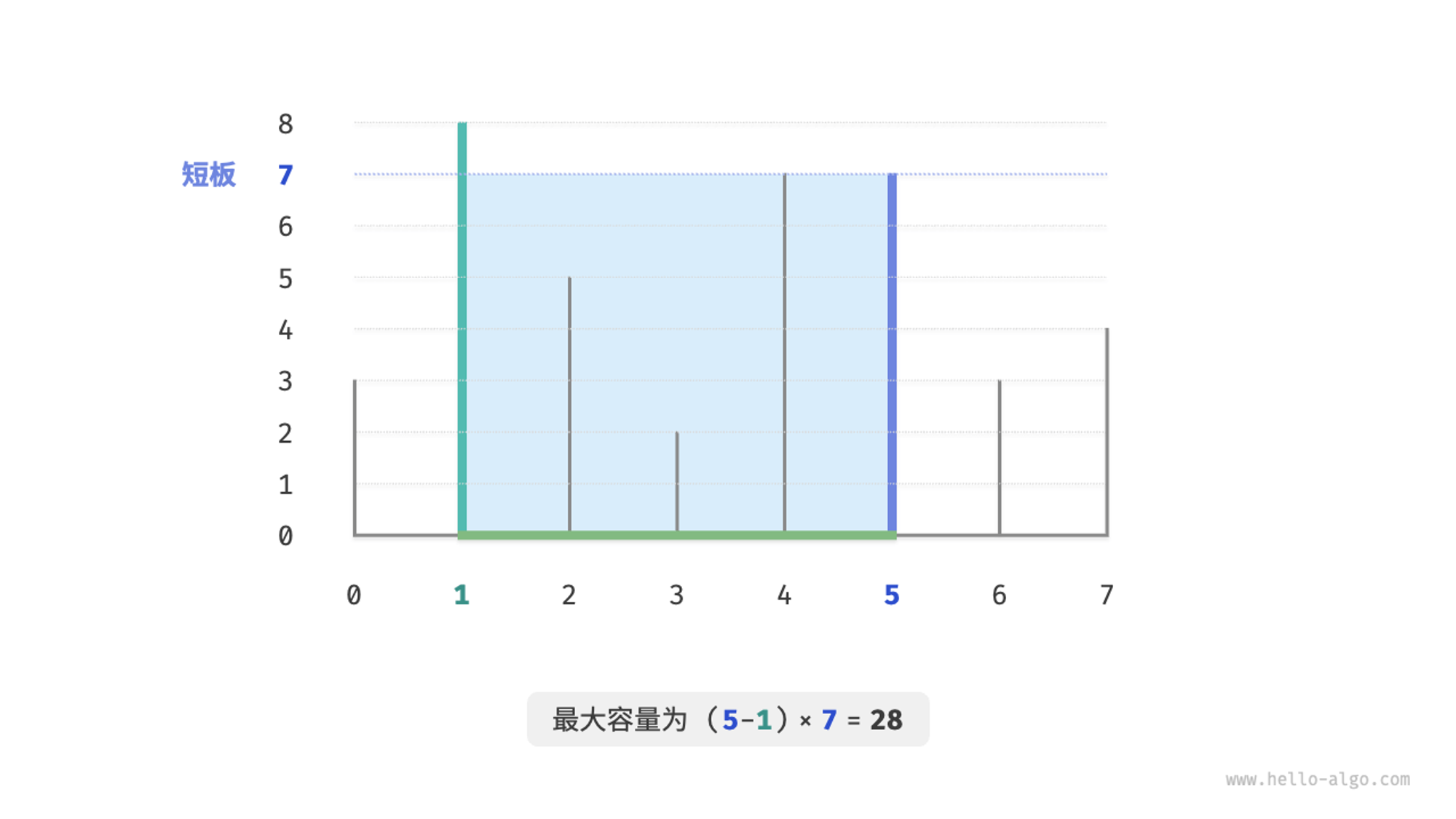
面对这个问题，我们最简单的方式就是做暴力，计算每两个柱子之间的容量和，我们可以直接用暴力破解。

tsx

function maxCapacity(ht: number[]): number {
  const n = ht.length;
  
  let max = 0;
  
  for (let i = 0; i < n - 1; i++) {
    for(let j = i + 1; j < n; j++) {
      const val = (j - i) * Math.min(ht[i], ht[j]);
      
      if(val > max) {
        max = val;
      }
    }
  }
  
  return max;
}

上方这里，我们可以看到时间复杂度为 O(n^2), 空间复杂度为 O(1)

但其实我们这里还可以使用贪心算法。

贪心策略确认

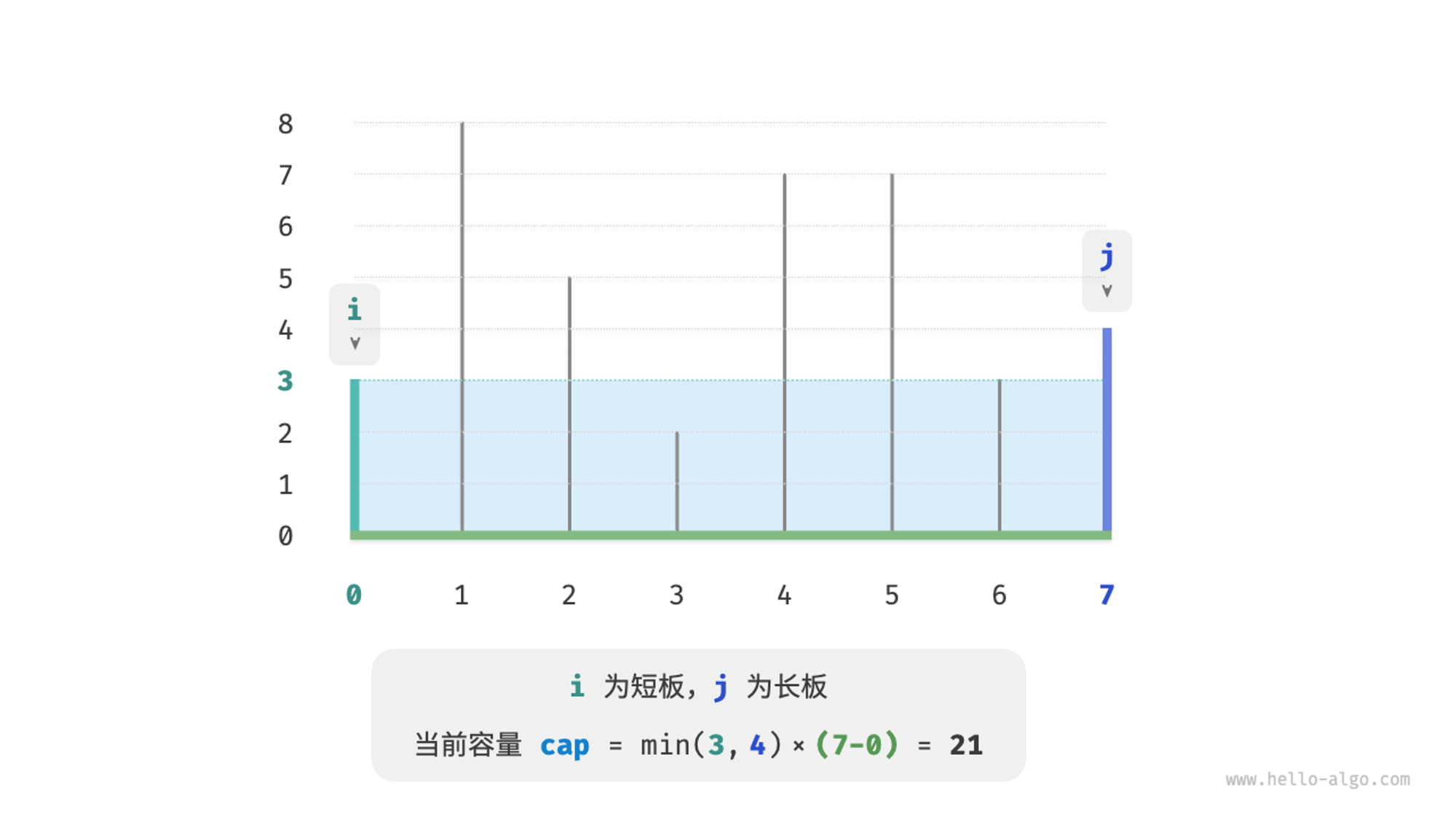
在过程中，我们一定会存在长板和短板。这个时候其实我们有两种选择，移动长板或移动短板

移动长板：移动过后的高度一定不会大于之前的高度，并且宽度一定是缩小的。
移动短板：高度不一定，宽度不一定，才有可能变大。

所以我们的策略是移动短板，去记录下最大值。

代码实现

代码循环最多 𝑛 轮，因此时间复杂度为 𝑂(𝑛) 。

变量 𝑖、𝑗、𝑟𝑒𝑠 使用常数大小的额外空间，因此空间复杂度为 𝑂(1) 。

tsx

function maxCapacity(ht: number[]): number {
  const n = ht.length;
  let i = 0, j = n - 1;
  let max = 0;
  
  
  while(i < j) {
    const cap = Math.min(ht[i], ht[j]) * (j - i);
    if(cap > max) {
      max = cap;
    }
    
    if(ht[j] < ht[i]) {
      j--;
    } else {
      i++;
    }
  }
  
  return max;
}

正确性证明

之所以贪心比穷举更快，是因为每轮的贪心选择都会“跳过”一些状态。

比如在状态 𝑐𝑎𝑝[𝑖,𝑗] 下，𝑖为短板、𝑗为长板。若贪心地将短板𝑖向内移动一格，会导致图 15-12 所示的状态被“跳过”。

这意味着之后无法验证这些状态的容量大小。

但其实我们已经推论了这些被跳过的状态实际上就是将长板 𝑗 向内移动的所有状态。前面我们已经证明内移长板一定会导致容量变小。也就是说，被跳过的状态都不可能是最优解，跳过它们不会导致错过最优解。

以上分析说明，移动短板的操作是“安全”的，贪心策略是有效的。

参考

https://www.hello-algo.com/chapter_greedy/max_capacity_problem/#3

最大容量问题 ​

贪心策略确认 ​

代码实现 ​

正确性证明 ​

参考 ​

最大容量问题

贪心策略确认

代码实现

正确性证明

参考