最大切分乘积问题

💡 给定一个正整数 𝑛，将其切分为至少两个正整数的和，求切分后所有整数的乘积最大是多少，如图 15-13 所示。

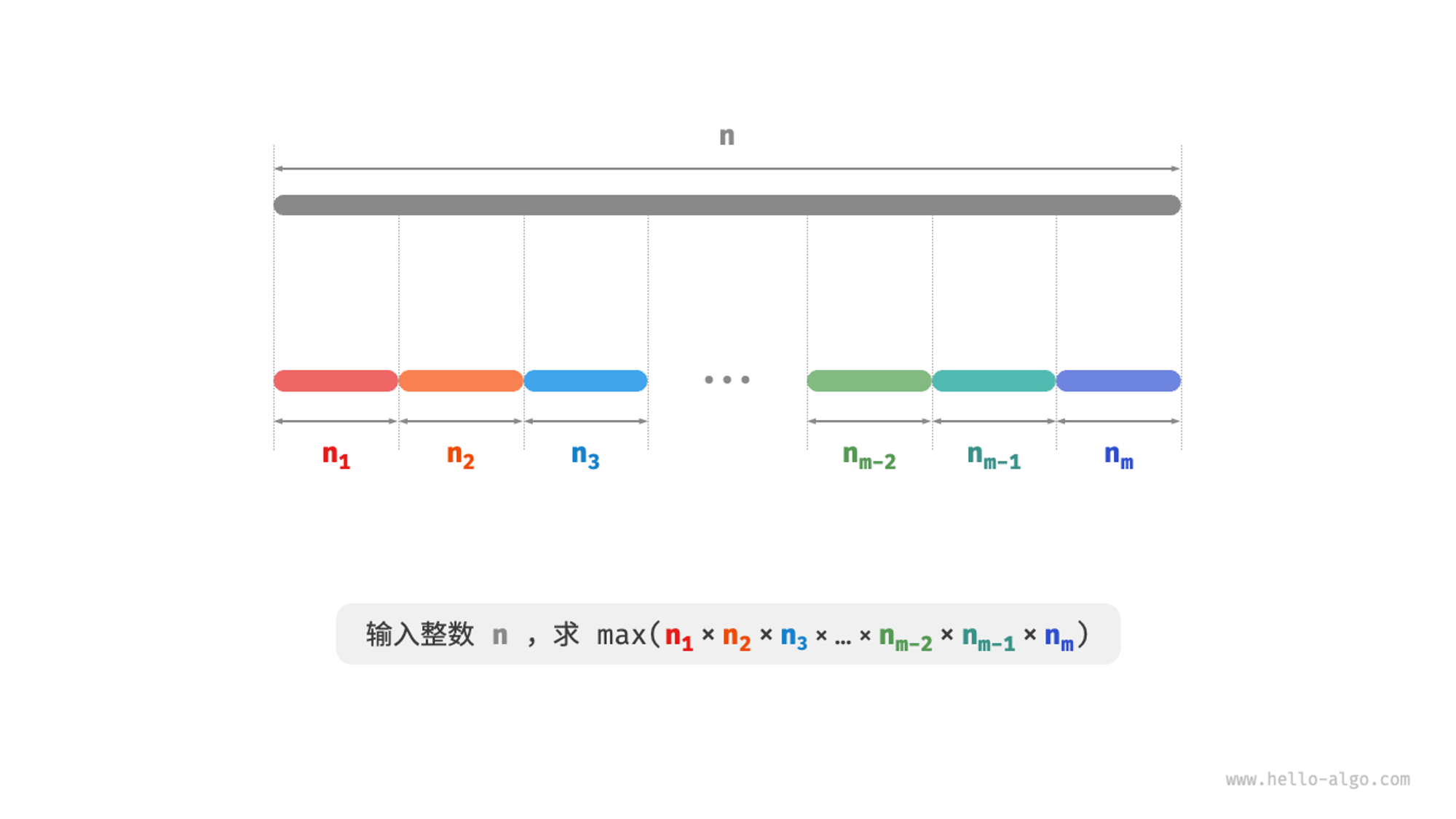
1. 贪心策略确定

根据经验，两个整数的乘积往往比他们的加和大，我们可以计算出边界条件。

2(n-2) >= n
n >= 4

如图 15-14 所示，当 𝑛≥4 时，切分出一个2后乘积会变大，这说明大于等于 4 的整数都应该被切分。

贪心策略一：如果切分方案中包含≥4的因子，那么它就应该被继续切分。最终的切分方案只应出现1、2、3这三种因子。

接下来思考哪个因子是最优的。在 1、2、3 这三个因子中，显然 1 是最差的，因为 1×(𝑛−1)<𝑛 恒成立，即切分出 1 反而会导致乘积减小。

如图 15-15 所示，当 𝑛=6 时，有 3×3>2×2×2 。这意味着切分出 3 比切分出 2 更优。

贪心策略二：在切分方案中，最多只应存在两个2。因为三个2总是可以替换为两个3，从而获得更大的乘积。

综上所述，可推理出以下贪心策略。

1. 输入整数 n ，从其不断地切分出因子  3，直至余数为 0、1、2。
2. 当余数为 0 时，代表 n 是 3 的倍数，因此不做任何处理。
3. 当余数为 2 时，不继续划分，保留。
4. 当余数为 1 时，由于 2 * 2 > 1 * 3 ，因此应将最后一个 3 替换为 2。

2. 代码实现

function maxProductCutting(n: number): number {
  if (n <= 3) {
    return 1 * (n - 1);
  }
  // 贪心地切分出 3 ，a 为 3 的个数，b 为余数
  let a: number = Math.floor(n / 3);
  let b: number = n % 3;
  if (b === 1) {
    // 当余数为 1 时，将一对 1 * 3 转化为 2 * 2
    return Math.pow(3, a - 1) * 2 * 2;
  }
  if (b === 2) {
    // 当余数为 2 时，不做处理
    return Math.pow(3, a) * 2;
  }
  return Math.pow(3, a);
}

时间复杂度取决于编程语言的幂运算的实现方法。以 Python 为例，常用的幂计算函数有三种。

• 运算符 * 和函数 pow() 的时间复杂度均为  𝑂(log⁡⁡𝑎)
• 函数 math.pow() 内部调用 C 语言库的 pow() 函数，其执行浮点取幂，时间复杂度为  𝑂(1)。

变量 𝑎 和 𝑏 使用常数大小的额外空间，因此空间复杂度为 𝑂(1) 。