动态规划问题特征
我们学习了动态规划是如何通过子问题分解来求解原问题的。实际上,子问题分解是一种通用的算法思路,在分治、动态规划、回溯中的侧重点不同。
- 动态规划:动态规划通过子问题分解来求解原问题,具体做法是:
- 将问题分解为多个子问题,解决每个子问题,并将其结果存储(通常使用数组或表格)以避免重复计算。
- 通过自底向上(或自顶向下)逐步解决子问题,最终合并这些结果以得到原问题的解。
- 侧重点在于存储和重用子问题的解(避免重复计算)。
- 分治算法:分治算法也采用子问题分解的方法,其步骤是:
- 将问题分解为若干个独立的、规模较小的子问题。
- 递归地解决这些子问题。
- 将子问题的解组合起来,得到原问题的解。
- 侧重点在于将问题分解为独立的子问题,并通过递归求解。
- 回溯算法:回溯算法也是通过子问题分解来求解原问题,其过程是:
- 将问题逐步分解,并尝试所有可能的选择(路径)。
- 递归地探索每个选择,当发现某个选择不符合要求时,回溯并尝试其他选择。
- 侧重点在于尝试和回溯所有可能的选择,寻找满足条件的解。
实际上,动态规划常用来求解最优化问题,它们不仅包含重叠子问题,还具有另外两大特性:最优子结构、无后效性。
最优子结构
我们对爬楼梯问题稍作改动,使之更加适合展示最优子结构概念。
题目:给定一个楼梯,你每步可以上1阶或者2阶,每一阶楼梯上都贴有一个非负整数,表示你在该台阶所需要付出的代价。给定一个非负整数数组𝑐𝑜𝑠𝑡,其中𝑐𝑜𝑠𝑡[𝑖]表示在第𝑖个台阶需要付出的代价,𝑐𝑜𝑠𝑡[0]为地面(起始点)。请计算最少需要付出多少代价才能到达顶部?
如图 14-6 所示,若第1、2、3阶的代价分别为1、10、1,则从地面爬到第3阶的最小代价为2
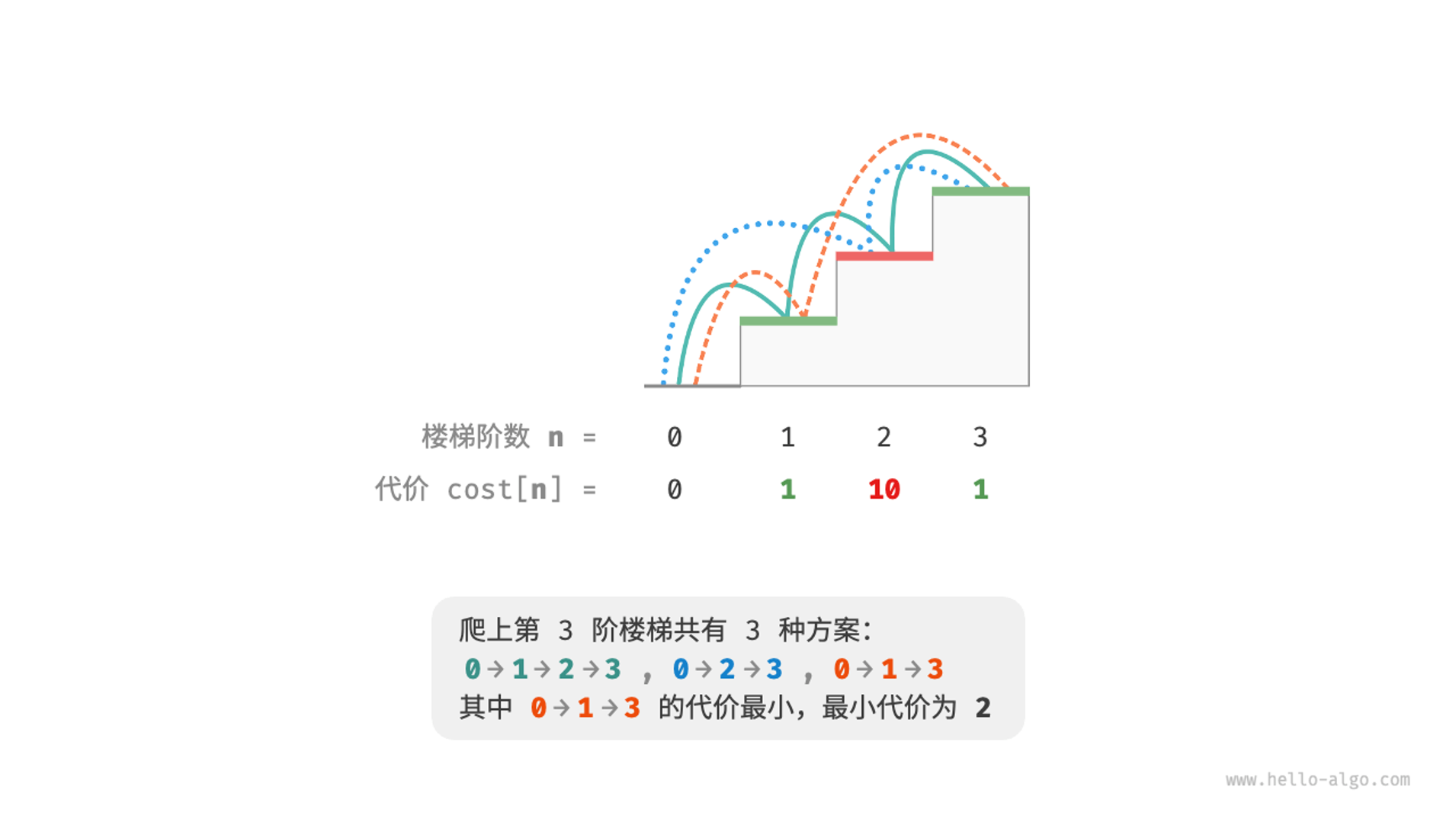
于是,我们可以推到出公式
tsx
dp[i] = min(dp[i - 1], dp[i - 2]) + cost[i]这便可以引出最优子结构的含义:原问题的最优解是从子问题的最优解构建得来的。
于是,我们可以根据来写算法,
tsx
function minCostClimbingStairsDP(cost: Array<number>): number {
const n = cost.length - 1;
if (n === 1 || n===2) {
return cost[n]
}
const dp = new Array(n + 1);
dp[1] = cost[1];
dp[2] = cost[2];
for(let i = 3; i <= n; i++) {
dp[i] = Math.min(dp[i-1], dp[i-2]) + cost[i];
}
return dp[n];
}其中,我们可以得到下方信息
- 初始状态:
dp[1]=cost[1]、dp[2]=cost[2] - 状态转移方程:
dp[i] = min(dp[i-1], dp[i-2]) + cost[i]
空间优化
tsx
function minCostClimbingStairsDP(cost: Array<number>): number {
const n = cost.length - 1;
if (n === 1 || n===2) {
return cost[n]
}
let a = cost[1], b = cost[2];
for(let i = 3; i <= n; i++) {
const tmp = b;
b = Math.min(a, tmp) + cost[i];
a = tmp;
}
return b;
}无后效性
无后效性是动态规划能够有效解决问题的重要特性之一,其定义为:给定一个确定的状态,当前阶段的状态一旦确定,就不再受未来阶段决策的影响。
无后效性主要体现在以下两个方面:
- 状态独立性:每一个状态的最优解只依赖于前一个阶段的状态,而不依赖于后续阶段的状态。这意味着我们在做决策时,只需要考虑当前状态及其之前的状态,而不必考虑未来的变化。
- 阶段独立性:问题被分解成多个子问题后,每个子问题的最优解不会影响其他子问题的求解。这种独立性使得子问题之间没有相互干扰,从而可以独立求解。
举个例子
以爬楼梯问题为例,给定状态𝑖,它会发展出状态𝑖+1和状态𝑖+2,分别对应跳1步和跳2步。在做出这两种选择时,我们无须考虑状态𝑖之前的状态,它们对状态𝑖的未来没有影响。
题目:给定一个共有𝑛阶的楼梯,你每步可以上1阶或者2阶,但不能连续两轮跳 1 阶,请问有多少种方案可以爬到楼顶?
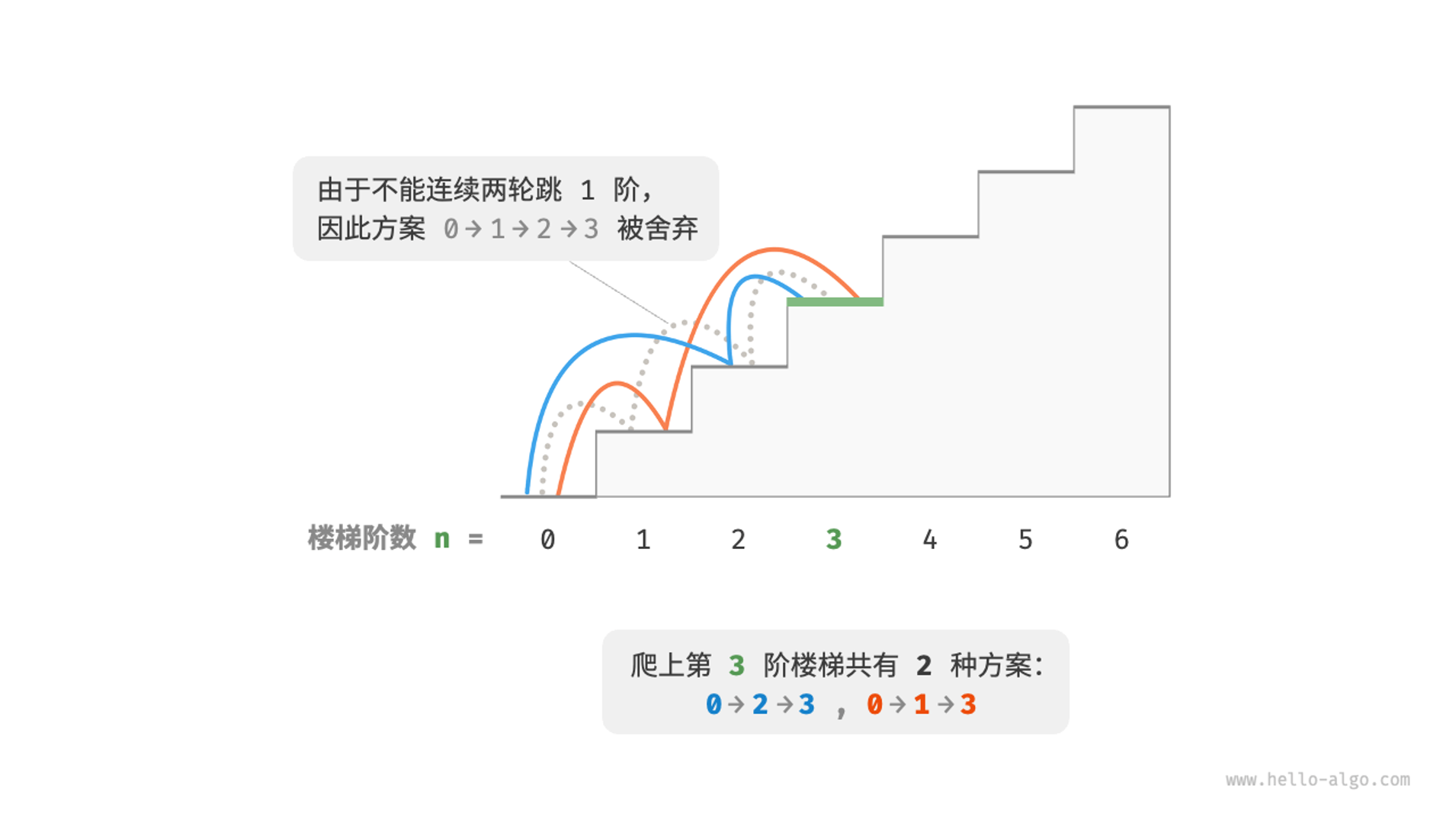
于是乎,我们的可能得用一个二维数据来进行 dp 计算了
则有
tsx
dp[i, 1] = dp[i-1, 2]
dp[i, 2] = dp[i-2, 1] + dp[i-2, 2]动态规划方程代码
tsx
function climbingStairsConstraintDP(n: number): number {
if (n === 1 || n === 2) {
return 1;
}
// 初始化 dp 表,用于存储子问题的解
const dp = Array.from({ length: n + 1 }, () => new Array(3));
// 初始状态:预设最小子问题的解
dp[1][1] = 1;
dp[1][2] = 0;
dp[2][1] = 0;
dp[2][2] = 1;
// 状态转移:从较小子问题逐步求解较大子问题
for (let i = 3; i <= n; i++) {
dp[i][1] = dp[i - 1][2];
dp[i][2] = dp[i - 2][1] + dp[i - 2][2];
}
return dp[n][1] + dp[n][2];
}在上个问题中,这个状态有过去的状态所决定,这符合无后效性。而结果由当前状态决定,符合马尔可夫过程。