动态规划解题思路

之前大概了解了什么是动态规划以及动态规划的特征。

下面我们来看看两个点

如何判断一个问题是不是动态规划问题
动态规划的解题流程是什么。

问题判断

如果一个问题满足：重叠子问题、最优子结构，无后效性。那么通常适用于动态规划求解。然而，这些特点并不是直接能看出来的，通常我们会先观察问题是否适合使用回溯（穷举）解决。

适合用回溯解决的问题通常满足“决策树模型”，这种问题可以使用树形结构来描述，其中每一个节点代表一个决策，每一条路径代表一个决策序列。（一个节点能表明一个状态）

换句话说，如果问题包含明确的决策概念，并且解是通过一系列决策产生的，那么它就满足决策树模型，通常可以使用回溯来解决。

在此基础上，动态规划问题还有一些判断的“加分项”。

最优子结构：问题包含最大（小）或最多（少）等最优化描述。
状态可传递：问题的状态能够使用一个列表、多维矩阵或树来表示，并且一个状态与其周围的状态存在递推关系。

相应地，也存在一些“减分项”。

问题的目标是找出所有可能的解决方案，而不是找出最优解。
问题描述中有明显的排列组合的特征，需要返回具体的多个方案。

如果一个问题满足决策树模型，并具有较为明显的“加分项”，我们就可以假设它是一个动态规划问题，并在求解过程中验证它。

问题求解步骤

动态规划的步骤主要包含下方5步：

描述决策
定义状态
建立 DP 表
推导状态转移方程
确认边界条件

为了更形象地展示解题步骤，我们使用一个经典问题“最小路径和”来举例。

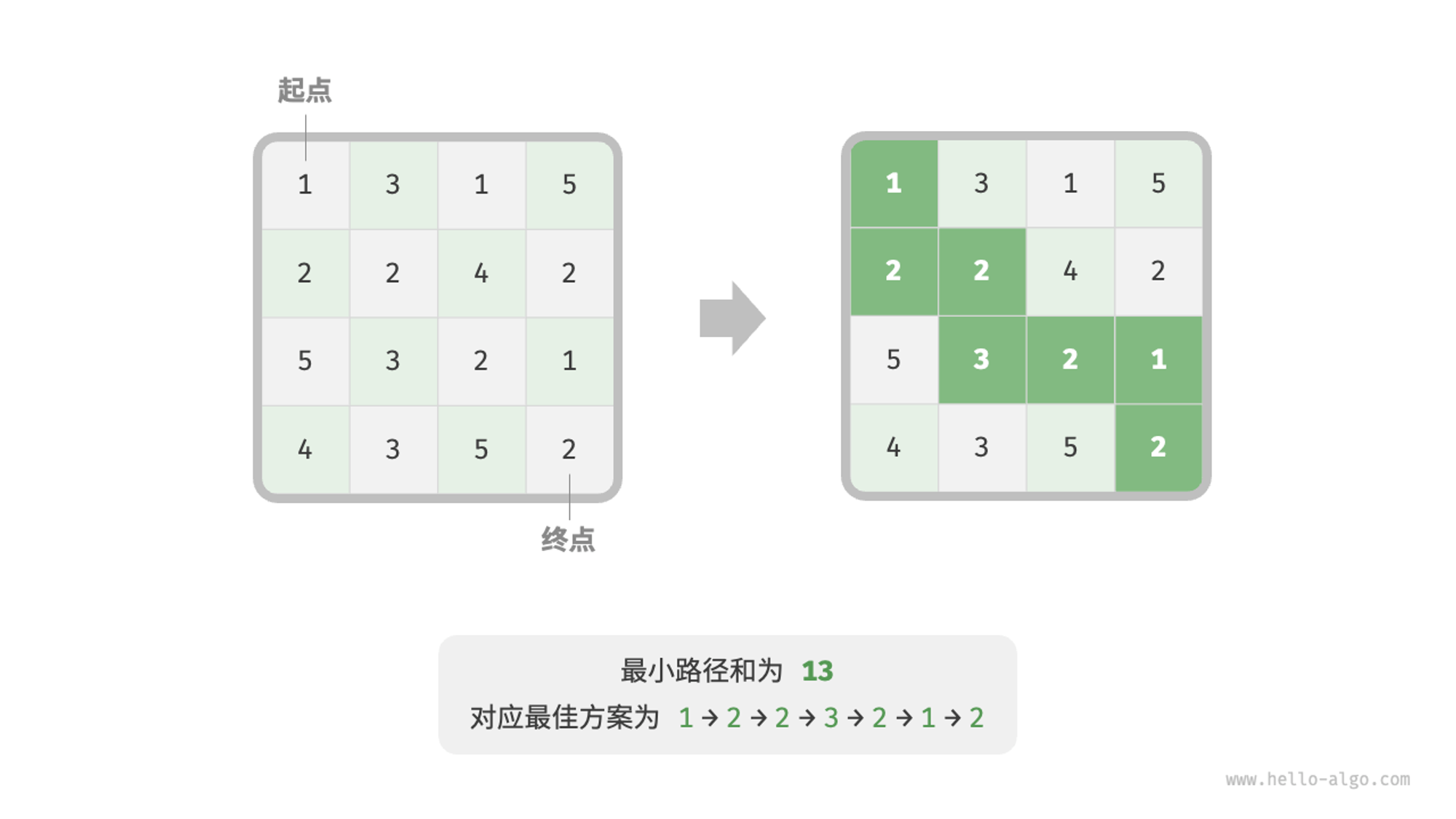
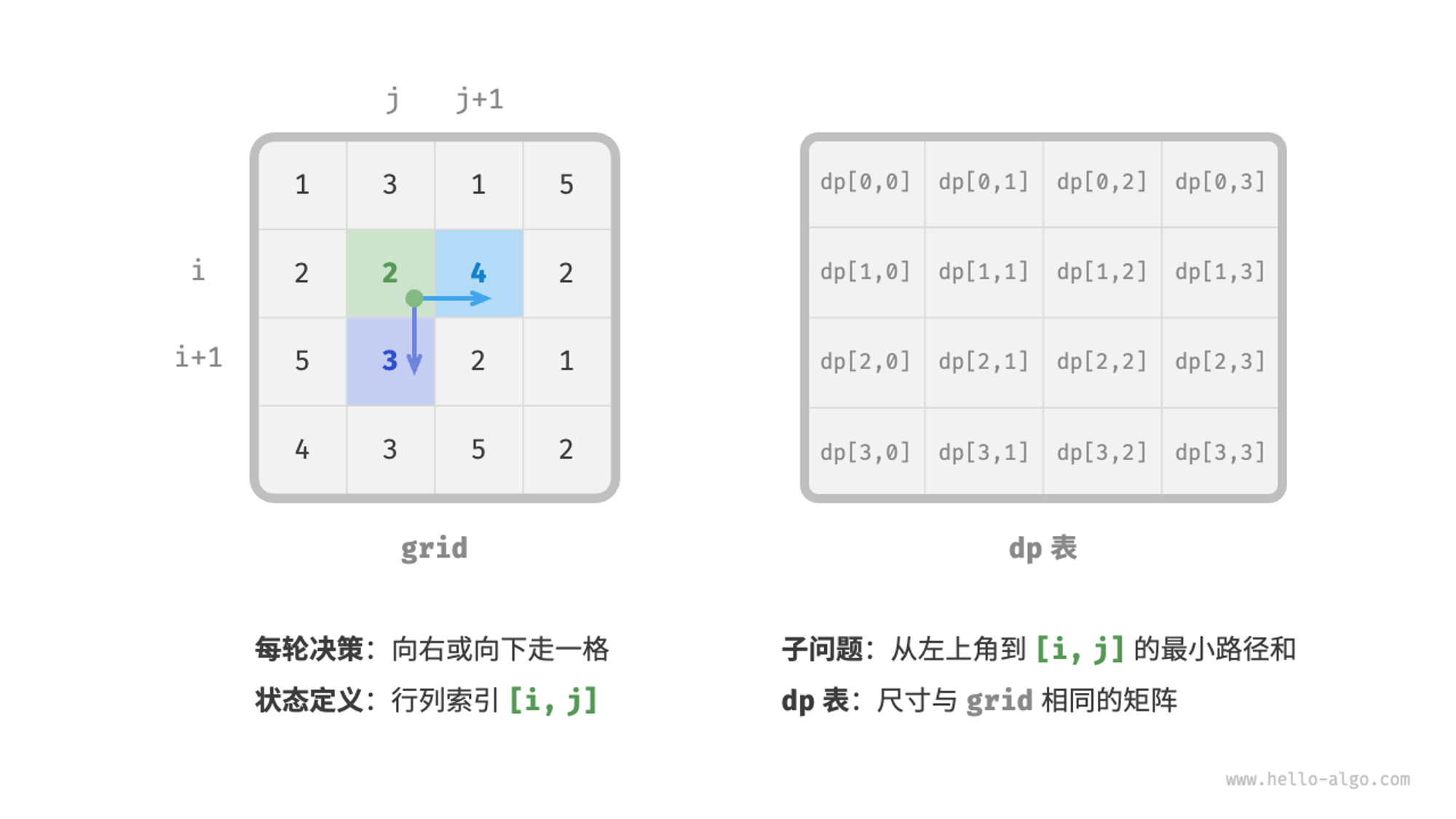
第一步：思考每轮的决策，定义状态，从而得到 𝑑𝑝 表

每一次决策就是从当前格子往下或往右走。则有，当前的索引如果为 [i, j], 则下一步则是 d[i+1, j] 或 d[i, j+1]。

状态 [𝑖,𝑗] 对应的子问题为：从起始点 [0,0] 走到 [𝑖,𝑗] 的最小路径和，解记为 𝑑𝑝[𝑖,𝑗] 。

至此，我们就得到了图 14-11 所示的二维 𝑑𝑝 矩阵，其尺寸与输入网格 𝑔𝑟𝑖𝑑 相同。

第二步：找出最优子结构，进而推导出状态转移方程

于是我们的状态转移方程就直接出来了

tsx

dp[i, j] = min(dp[i -1, j], dp[i, j - 1]) + grid[i, j]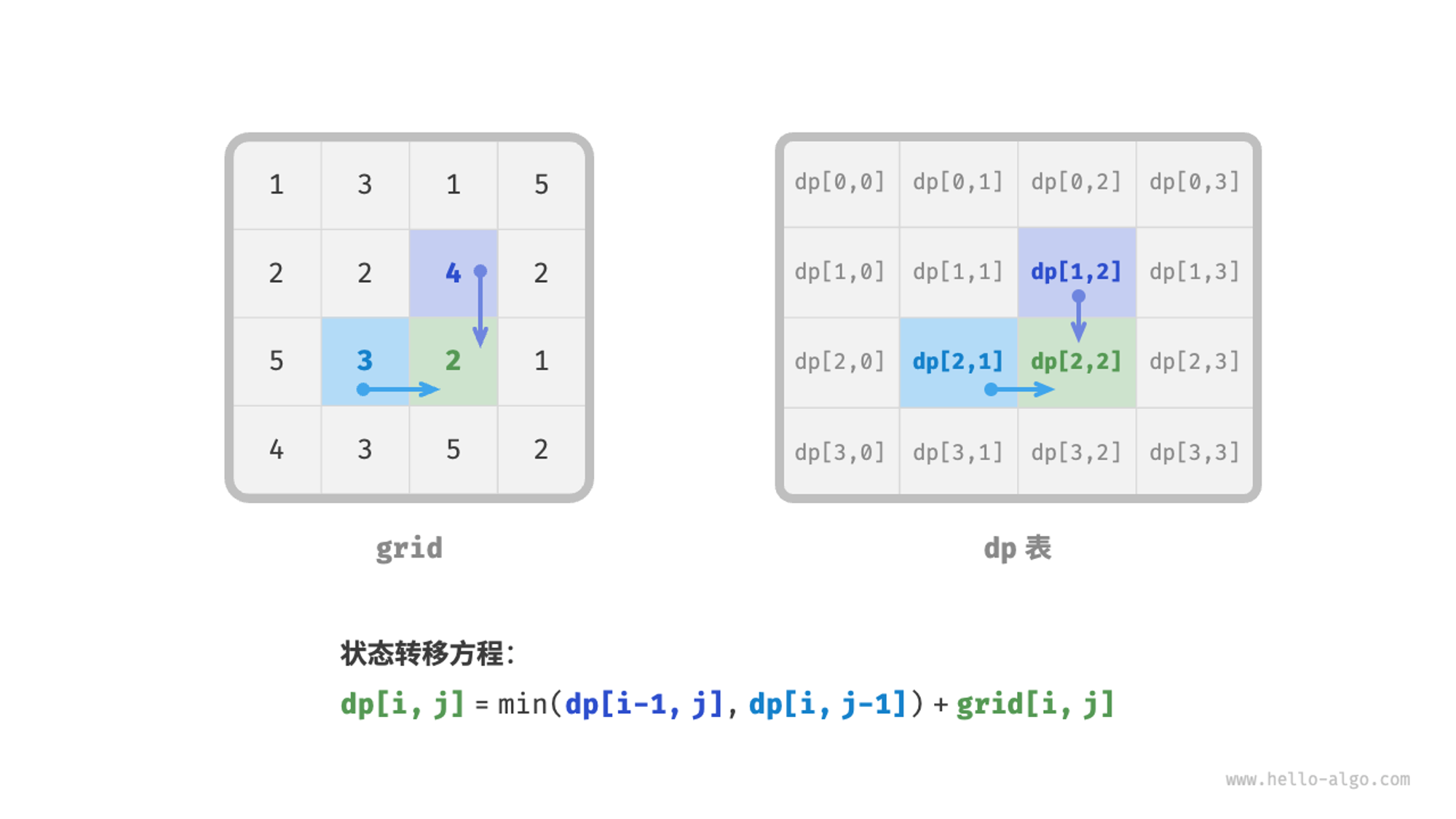

第三步：确定边界条件和状态转移顺序

在本题中，处在首行的状态只能从其左边的状态得来，处在首列的状态只能从其上边的状态得来，因此首行 𝑖=0 和首列 𝑗=0 是边界条件。

如图 14-13 所示，由于每个格子是由其左方格子和上方格子转移而来，因此我们使用循环来遍历矩阵，外循环遍历各行，内循环遍历各列。

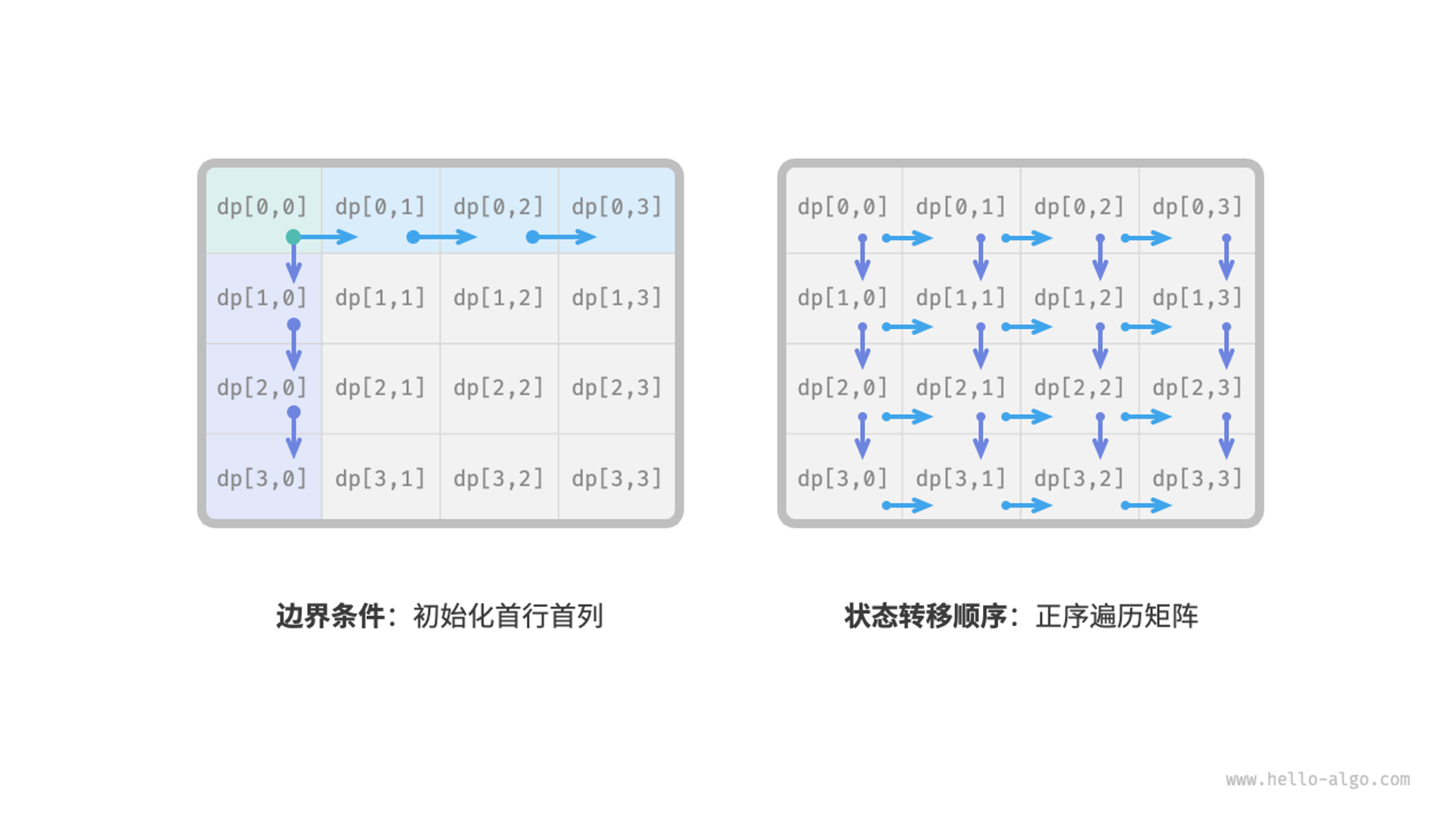
其实这个时候，我们已经能写出动态规划的代码了，但我们还是从暴力 → 记忆化 → 动态规划来实现看看吧。

暴力算法

从状态 [𝑖,𝑗] 开始搜索，不断分解为更小的状态 [𝑖−1,𝑗] 和 [𝑖,𝑗−1] ，递归函数包括以下要素。

递归参数：状态[𝑖,𝑗] 。
返回值：从 [0,0] 到 [𝑖,𝑗] 的最小路径和 𝑑𝑝[𝑖,𝑗] 。
终止条件：当 𝑖=0 且𝑗=0 时，返回代价 𝑔𝑟𝑖𝑑[0,0]。
剪枝：当 𝑖<0 时或 𝑗<0时索引越界，此时返回代价 +∞ ，代表不可行。

实现代码如下：

tsx

const minPathSumDFS = (
  grid: number[][],
  i: number,
  j: number
) => {
  if(i === 0 && j === 0) {
    return grid[0][0]
  }
  
  if (i < 0 || j < 0) {
    return Infinity;
  }
  
  const up = minPathSumDFS(grid, i, j - 1);
  const left = minPathSumDFS(grid, i - 1, j);
  
  return Math.min(up, left) + grid[i][j];
}

但这个过程为出现比较多重复的子问题，在这个代码中会被重新进行计算。

每个状态都有向下和向右两种选择，从左上角走到右下角总共需要𝑚+𝑛−2步，所以最差时间复杂度为𝑂(2𝑚+𝑛)

记忆化

实质上是用一个数组来进行存储。

tsx

const minPathSumDFS = (
  grid: number[][],
  mem: number[][],
  i: number,
  j: number
) => {
  if(i === 0 && j === 0) {
    return grid[0][0]
  }
  
  if (i < 0 || j < 0) {
    return Infinity;
  }
  
  if(mem[i][j]) {
    return mem[i][j]
  }
  
  const up = minPathSumDFS(grid, i, j - 1);
  const left = minPathSumDFS(grid, i - 1, j);
  
  const res = Math.min(up, left) + grid[i][j];
  mem[i][j] = res;
  
  return res;
}

动态规划

tsx

function minPathSumDP(grid: Array<Array<number>>): number {

  const n = grid.length, m = grid[0].length;
  // 初始化 dp 表
  const dp = Array.from({ length: n }, () =>
    Array.from({ length: m }, () => 0)
  )

  const dp: number[][] = [];
  dp[0][0] = grid[0][0];
  
  for(let i = 1; i < n; i++) {
    dp[i][0] = dp[i-1, 0] + grid[i][0];
  }
  
  for(let j = 1; j < n; j++) {
    dp[0][j] = dp[0, j-1] + grid[0][j];
  }
  
  for(let i = 1; i < n; i++) {
    for (let j: number = 1; j < m; j++) {
      dp[i][j] = Math.min(dp[i][j - 1], dp[i - 1][j]) + grid[i][j];
    }
  }
  
  return dp[n-1][m-1];
}

图 14-16 展示了最小路径和的状态转移过程，其遍历了整个网格，因此时间复杂度为 𝑂(𝑛𝑚) 。

数组 dp 大小为 𝑛×𝑚 ，因此空间复杂度为 𝑂(𝑛𝑚) 。

参考

https://www.hello-algo.com/chapter_dynamic_programming/dp_solution_pipeline/

问题判断 ​

问题求解步骤 ​

暴力算法 ​

记忆化 ​

动态规划 ​

参考 ​

问题判断

问题求解步骤

暴力算法

记忆化

动态规划

参考