初识动态规划

动态规划的核心是利用最优子结构，通过存储子问题的解，避免重复计算，从而有效地解决问题。

动态规划（Dynamic Programming，简称DP）是一种用于解决复杂问题的方法，通过将问题分解成更小的子问题来解决。它常用于优化问题，特别是那些可以通过分解成重叠子问题和最优子结构的方式来解决的问题。下面是理解动态规划的一些关键点和步骤：

动态规划的基本思想

分解问题：将原问题分解成相互重叠的子问题。
解决子问题：从最简单的子问题开始逐步解决每个子问题。
存储子问题的解：将每个子问题的解存储在一个表格（如数组或矩阵）中，以避免重复计算。
组合子问题的解：根据子问题的解来构建原问题的解。

关键概念

最优子结构：一个问题的最优解包含其子问题的最优解。
子问题重叠：不同的子问题之间会有重叠部分，即相同的子问题会被多次计算。
状态转移方程：通过状态转移方程描述从一个状态到另一个状态的关系，用来定义子问题之间的联系。

具体例子

给定一个共有 𝑛 阶的楼梯，你每步可以上 1 阶或者 2阶，请问有多少种方案可以爬到楼顶？

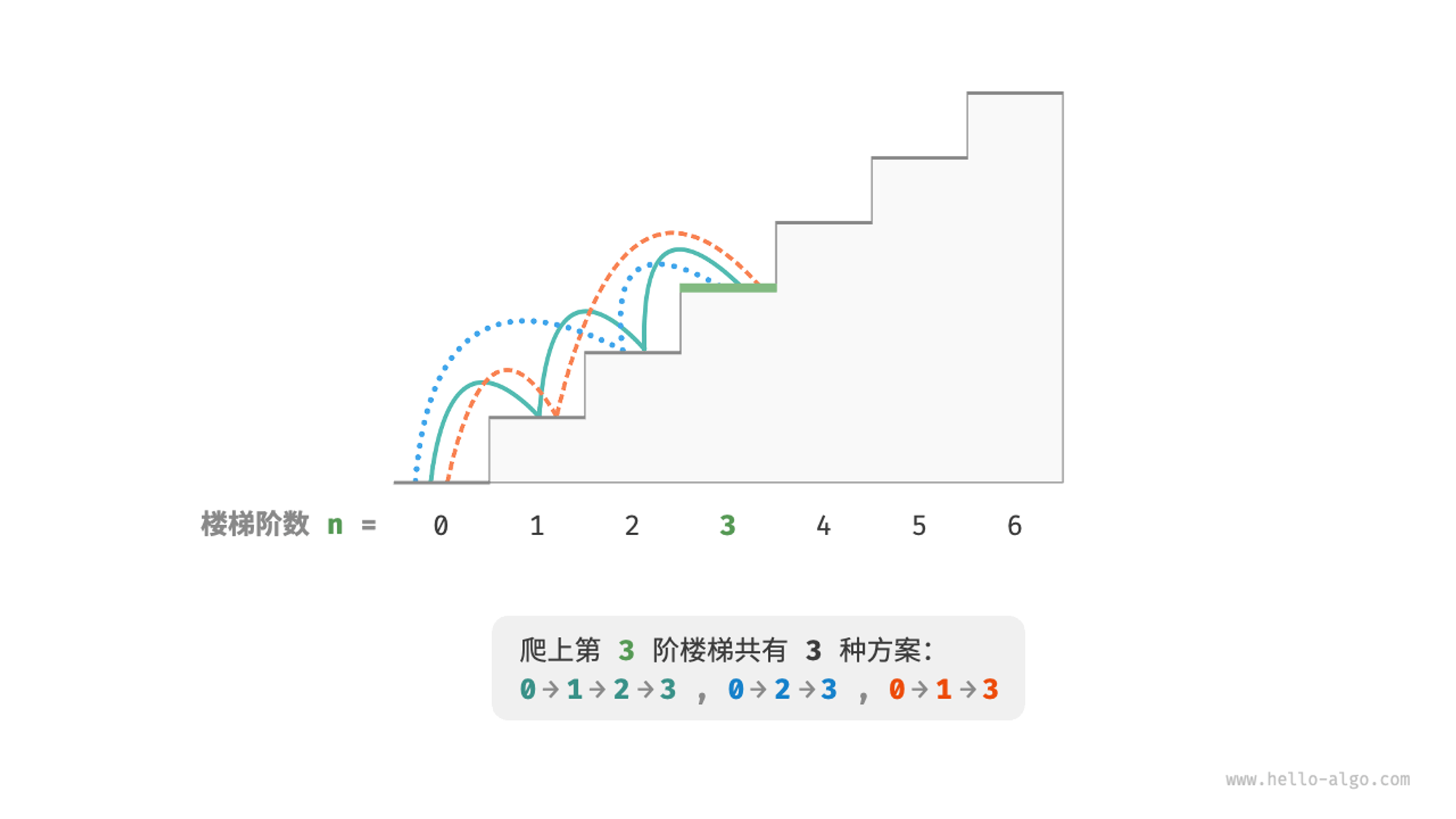
在这里，我们其实可以发现，需要到达第 i 层的话并且 i > 2，只能由两种情况，即从第 i-1 层走 1 步，或者从 i-2 层走两步。

所以有如下规律：

当 i ≤ 2 的时候: 则有 dp[1] =1, dp[2] = 2
当 i > 2 的时候：则由 dp[i] = dp[i-2] + dp[i-1]

于是，我们目前可以用递归暴力的方法，来解。

递归暴力

tsx

/* 爬楼梯：搜索 */
function climbingStairs(n: number): number {
  if(n === 1 || n === 2) {
    return n;
  }
  return climbingStairs(n - 1) + climbingStairs(n - 2);
}

当在这里，我们会发现，由于每次都会新增两次运算，所以这里的时间复杂度为 O(2^i)，于是我们看了下，是不是有些东西可以做存储，比如说已经知道 climbingStairs(2)，是不是可以缓存起来。

记忆化搜索

思路很简单，用一个数组将结果进行存储即可。

tsx

/* 记忆化搜索 */
function dfs(i: number, mem: number[]): number {
    // 已知 dp[1] 和 dp[2] ，返回之
    if (i === 1 || i === 2) return i;
    // 若存在记录 dp[i] ，则直接返回之
    if (mem[i] != -1) return mem[i];
    // dp[i] = dp[i-1] + dp[i-2]
    const count = dfs(i - 1, mem) + dfs(i - 2, mem);
    // 记录 dp[i]
    mem[i] = count;
    return count;
}

/* 爬楼梯：记忆化搜索 */
function climbingStairsDFSMem(n: number): number {
    // mem[i] 记录爬到第 i 阶的方案总数，-1 代表无记录
    const mem = new Array(n + 1).fill(-1);
    return dfs(n, mem);
}

于是，这块，我们每次子问题只需要计算一遍，则为 O(n)。

动态规划

记忆化搜索是一种“从顶至底”的方法：我们从原问题（根节点）开始，递归地将较大子问题分解为较小子问题，直至解已知的最小子问题（叶节点）。之后，通过回溯逐层收集子问题的解，构建出原问题的解。

与之相反，动态规划是一种“从底至顶”的方法：从最小子问题的解开始，迭代地构建更大子问题的解，直至得到原问题的解。

由于动态规划不包含回溯过程，因此只需使用循环迭代实现，无须使用递归。在以下代码中，我们初始化一个数组 dp 来存储子问题的解，它起到了与记忆化搜索中数组 mem 相同的记录作用：

tsx

/* 爬楼梯：搜索 */
function climbingStairs(n: number): number {
  if(n === 1 || n === 2) return n; 
  const dp = new Array(n + 1).fill(-1);
  dp[1] = 1;
  dp[2] = 2;
  for(let i = 3; i <= n; i++) {
    dp[i] = dp[i-1] + dp[i-2];
  }
  return dp[n];
}

与回溯算法一样，动态规划也使用“状态”概念来表示问题求解的特定阶段，每个状态都对应一个子问题以及相应的局部最优解。例如，爬楼梯问题的状态定义为当前所在楼梯阶数 𝑖 。

根据以上内容，我们可以总结出动态规划的常用术语。

将数组 dp 称为 dp 表， dp[i] 表示状态 i 对应子问题的解
将最小子问题对应的状态（第 1 阶和第 2 阶楼梯）称为初始状态
将递推公式 𝑑𝑝[𝑖]=𝑑𝑝[𝑖−1]+𝑑𝑝[𝑖−2] 称为状态转移方程

空间优化

tsx

/* 爬楼梯：空间优化后的动态规划 */
function climbingStairsDPComp(n: number): number {
    if (n === 1 || n === 2) return n;
    let a = 1,
        b = 2;
    for (let i = 3; i <= n; i++) {
        const tmp = b;
        b = a + b;
        a = tmp;
    }
    return b;
}

在动态规划问题中，当前状态往往仅与前面有限个状态有关，这时我们可以只保留必要的状态，通过“降维”来节省内存空间。这种空间优化技巧被称为“滚动变量”或“滚动数组”。

参考

https://www.hello-algo.com/chapter_dynamic_programming/intro_to_dynamic_programming/

初识动态规划 ​

动态规划的基本思想 ​

关键概念 ​

具体例子 ​

递归暴力 ​

记忆化搜索 ​

动态规划 ​

参考 ​